Getting Cozy with Boolean Algebra
- Zoe Chowdhury
- Nov 27, 2023
- 5 min read
Updated: Mar 30, 2024
Think about it, it’s almost December, the air is getting colder and the leaves are falling – what better time to cuddle up on the couch and learn about Boolean algebra? (I hope you can tell I’m joking).
In the last article, we discussed how logic gates work and how to make a simple circuit with a logic gate. But what about when things aren’t so simple?
How do you tell someone that you want to make a circuit that goes like this:
You have 6 variables: a, b, c, d, e, and f. You want a AND b OR c AND d OR e OR NOT f.
The person would look at you like “…what?"
So, the next thing we would try is to show this person a diagram of what we want:

Then they would say, “Oh, you were trying to say (a*b)+(c*(d+e))+(~f)” in this totally real, not made-up scenario we all run into almost all the time. And this interaction would be your introduction to the importance of Boolean algebra.
Essentially, Boolean algebra allows us to be able to easily express how we want to manipulate our binary data inside digital systems. Much like regular algebra, it has symbols, rules, and identities that allow us to create complex Boolean functions that reflect our logic diagrams.
The Basics
Symbols
Here are the common symbols used in most equations:

Truth Tables
A truth table is used to run through every possible case of inputs that your function could have – allowing you to see all the possible results of the circuit you are trying to build.
Here are the truth tables for the basic operators:
AND

OR

NOT

Order of Operations
Much like how we use BEDMAS with regular algebra, Boolean algebra also follows an order of operations:

Rules
Now to make life easier, here are a few things we know will always be true when using Boolean algebra:
It’s associative, meaning: (x*y)*z=x*(y*z) and (x+y)+z=x+(y+z)
It’s commutative: x*y=y*x and x+y=y+x
It’s distributive: x*(y+z)=xy+xz and x+(y*z)=(x+y)*(x+z)
Simplification Rules
Then there are a bunch of other simplification rules that also come in handy:

This article barely scratches the surface of Boolean algebra so if you are interested in learning more about it, I recommend reading Chapter 2 of Digital Design 5th edition by M. Morris Mano (I’ll send you a digital copy of it if you ask through my website). So, with this information, we are going to move on to creating Boolean functions out of nothing but truth tables.
Boolean Functions
A Boolean function can be expressed algebraically from a truth table as a combination of one of the following:
1. The Sum of Products of the Minterms (SoP)
2. The Product of Sums of the Maxterms (PoS)
To explain these concepts, say we are given the following truth table and asked to create a circuit of it:
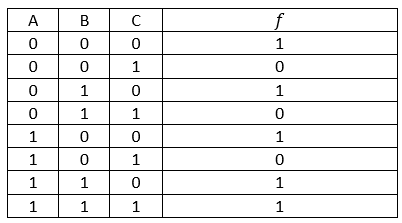
There is only so much we can do with a table of 1s and 0s, so the first thing we need to do is create an equation that represents this truth table.
The first way we can do that is by OR-ing all the terms that give us a result of 1.
The Sum of Products of the Minterms (SoP) Method
If we were to take the product of the terms A*B*C when A = 0, B = 0, and C = 0 – what kind of circuit could we run those inputs through to get 1? A circuit that negates all the terms such that (~A)*(~B)*(~C). So when 0 0 0 goes through our function, we would get 1. Now, if we make a similar circuit for each combination of inputs that we want to result in 1 and then combine them to say, "We just need this circuit OR this circuit OR this circuit... to give us a 1". Then since 1 OR anything is equal to 1 (based on the simplification rules above), the function would result in 1. This means we cover all the cases when the function should be equal to 1.
This is what that process looks like:
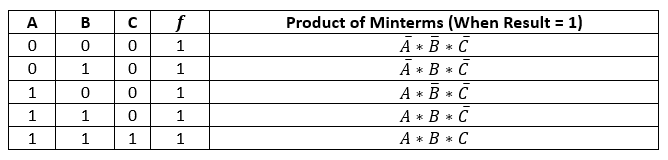
Therefore, we are saying one possible Boolean function that represents the truth table above is the following:
f = ((~A)*(~B)*(~C))+((~A)*(B)*(~C))+((A)*(~B)*(~C))+((A)*(B)*(~C))+((A)*(B)*(C))
So, what does this function mean really? By using the OR operator, we are saying we need at least a minimum of one of these minterms to be equal to 1 at any given time for the whole function to spit out 1. We can also see that this function will return 0 for every case where the result should be 0:

Another way we could go about this is by AND-ing all of the terms that give us a result of 0.
The Product of Sums of the Maxterms (PoS) Method
Now, if we were to take the sum of the terms A+B+C when a = 0, b = 0, and c = 1, how could we make a circuit that gives us a result of 0? Knowing that if any of the terms are equal to 1 then the whole result will be 1, we can do this by negating c such that A+B+(~C). Remember that when we AND something, if any of the terms are equal to 0, the whole function is equal to 0. Therefore, when we combine these circuits and say "We need this circuit AND this circuit AND this circuit... to be able to get a result of 0 every time it appears in the truth table".
Then that process looks like this:

Therefore, we are saying another possible Boolean function that represents the truth table above is the following:
f = ((A)+(B)+(~C))*((A)+(~B)+(~C))*((~A)+(B)+(~C))
Now, this function says that to get a result of 1, all the maxterms must be equal to 1 due to the AND operator. This means the maximum amount of terms in the function needs to be equal to 1 to get a result of 1, otherwise, you will get a result of 0.
Boolean functions expressed as a Sum of Minterms or Product of Maxterms are said to be in canonical (standards) forms.
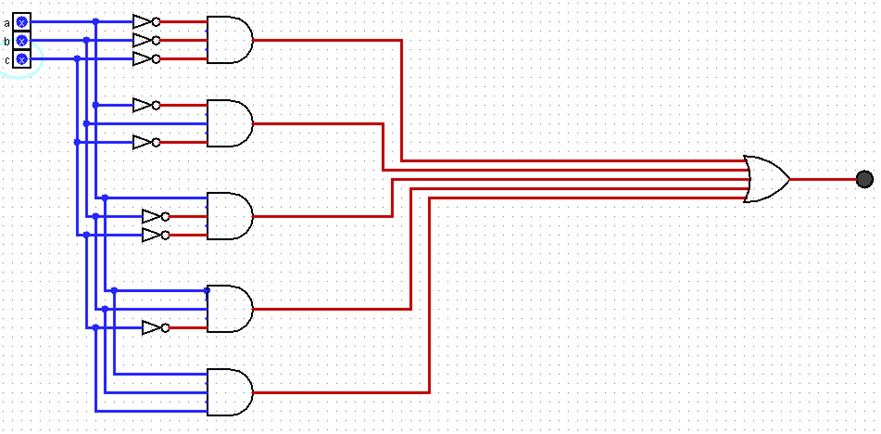
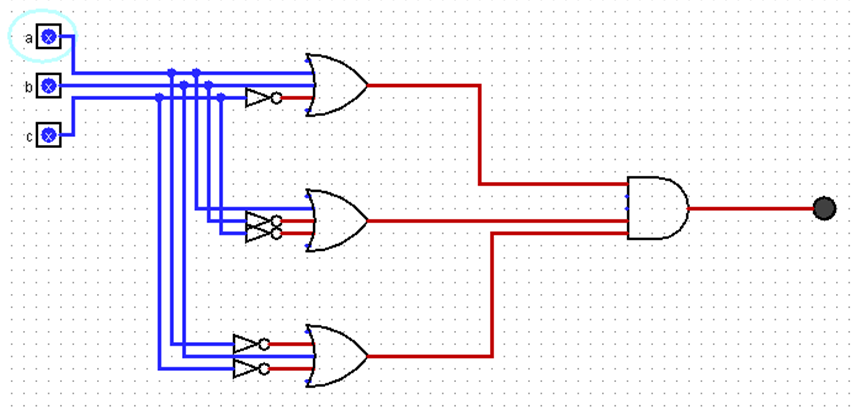
As you look at these two diagrams – which one do you think is cheaper and easier to implement? I don't know, let's try building them. This week, I made a video where I actually made these two circuits and provided an effort and cost breakdown of each option:
But we can do better than this. What if I told you this truth table is for a circuit with only three single variable terms? Then you will realize why we'll be discussing simplifying Boolean functions in next week's article.



Comments